From our orbital- absolute
magnitude distribution model, we can easily compute the expected density
of NEOs
in the various regions of the sky, as well as their apparent
magnitude and rates of motion.
 |
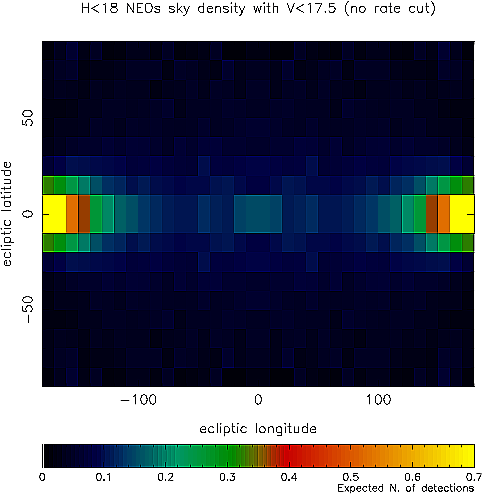The sky density of NEOs with
absolute magnitude H<18 and apparent magnitude V<17.5.
The colors indicate the expected number of detections in each 10x10 degree
cell.
Coordinates are in ecliptic latitude and longitude. Opposition is at (0,0), while the position of the Sun is at (-180,0) and (180,0). Notice that the NEO density has a local maximum near opposition, but the absolute maximum density occurs near the position of the Sun. Unfortunately, we cannot easily take advantage of this latter maximum, because ground based surveys have difficulty observing close to the Sun. |
Using this NEO density chart, we can investigate which survey strategies are capable of finding the largest number of NEOs.
The current NEO discovery record
is dominated by the LINEAR
survey. To evaluate their prospects for future NEO discoveries, we
have developed a software simulator that mimics LINEAR's methods and properties.
 |
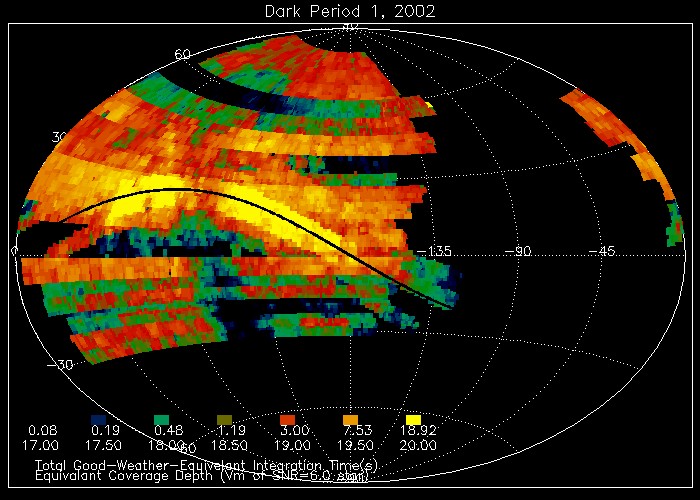An example of LINEAR's monthly sky coverage (from their website). Using this kind of information, we have defined the sky coverage for our LINEAR survey simulator. Our analysis of the discoveries reported by LINEAR suggested that LINEAR's limiting magnitude is, on average, V=18.5. Our survey simulator modeled this by assuming 100% discovery efficiency up to V=17.75, and a linear drop to 0% efficiency at V=19.25. We also adopted LINEAR's typical minimum rate of motion for NEO discoveries of 0.3deg/day. |
Our survey simulator does a remarkably good job at reproducing the performance of the LINEAR survey. We have tested our results in two ways:
TEST # 1:
| 273 NEOs with H<18 were known before January 1st, 1999, the appoximate date LINEAR began its search for NEOs. Starting from that date, LINEAR discovered 176 new H<18 NEOs over the next 2 years. Our survey simulator takes 2.3 years to increase the number of detected objects from 273 to 449, nearly the same amount of time. |
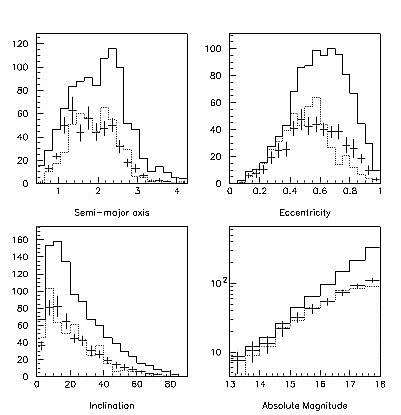
TEST #2:
| Our survey simulator does a good job at reproducing the orbital and absolute magnitude distribution of the 469 NEOs with H<18 which were discovered as of March 15, 2001. In this figure, the solid line represents the (a,e,i,H) distribution of NEOs according to our model. The points with (1 sigma) error bars give the distribution of the NEOs detected by our survey simulator over several different runs.The dotted line represents the distribution of the NEOs with H<18 discovered as of 15 March 2001. |  |
Using our survey simulator we can investigate what
are the prospects for achieving the Spaceguard goal of discovering
90% of the NEOs with H<18 within the next 6 years. Unfortunately,
our predictions are quite discouraging:
 |
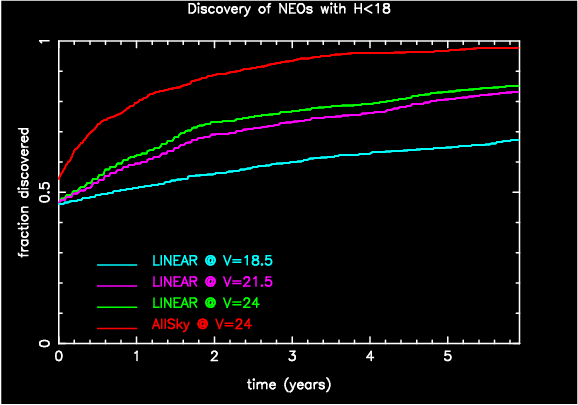The expected observational completeness of the H<18 NEO population during the next 6 years due to the LINEAR survey (cyan curve). The magenta and the green curves show how the situation would be improved if LINEAR's limiting magnitude were pushed to 21.5 and 24.0 respectively, with the same monthly sky coverage. The red curve shows the ideal case of a survey covering the entire sky visible at night, up to a limiting magnitude V=24. It is unclear how the proposed LSST survey will approach this ideal limit. |
As illustrated by the above figure (compare the V=21.5 and V=24 curves), increasing the limiting magnitude too much is useless unless the sky coverage is also increased to include regions of the sky close to the Sun. In fact, for a survey searching at opposition, pushing the limiting magnitude to higher values is equivalent to pushing out the distance where H<18 NEOs can be detected. However this does not help because, according to our model, most (85%) of the NEOs have aphelion distances smaller than 4.5 AU.
The situation is even more discouraging if one wishes
to extend the Survey goal to the NEOs (or PHOs)
with H<20.5 (i.e., the bodies capable of producing 1,000 megaton
impact energies when striking the Earth). In this case, it would be necessary
to have a LINEAR-like system with limiting magnitude of at leastV=24,
in order to achieve ~90% completeness within the next 6 years.
 |
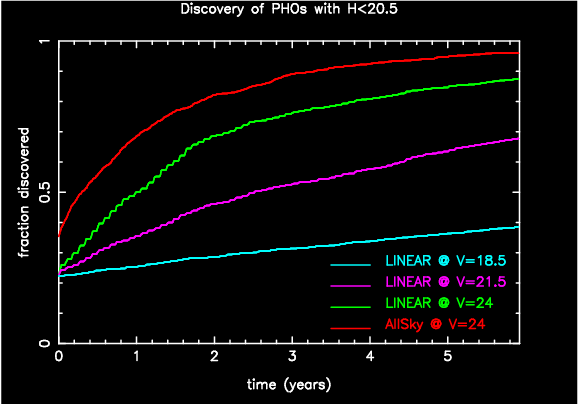The expected observational completeness of the Potentially Hazardous Objects with H<20.5 during the next 6 years due to the LINEAR survey (cyan curve). The magenta and the green curves show how the situation would be improved if LINEAR's limiting magnitude were pushed to 21.5 and 24.0 respectively, with the same monthly sky coverage. The red curve shows the ideal case of a survey covering the entire sky visible at night, up to a limiting magnitude V=24. |