Most numerical simulations of the geodynamo are cast in spherical
geometry, using a spherical harmonic
representation for lateral variations and an expansion in Chebyshev
polynomials or discretisation in radius. A number
of research groups have produced time dependent, three dimensional,
self-consistent solutions to the geodynamo
problem using this pseudospectral methodology. Computational
limitations currently place a practical bound on the
parameter regime that can be explored in this context, with values
appropriate for Earth out of reach by several orders
of magnitude. For the spherically pseudospectral codes, the absence of
an efficient Legendre transform is a strong
factor contributing to this limitation. As a first step towards
alternative computational methods for geodynamo
modelling, we have adapted an existing, efficiently parallelised
magnetohydrodynamics (MHD) code, originally
developed for weakly compressible, turbulent astrophysical MHD
problems. The Pencil Code
(
www.nordita.dk/data/brandenb/pencil-code)
is a Cartesian code that uses sixth-order finite differences, applied to
``pencils'' (i.e. array sections) in the x direction in a
cache-efficient way. The domain is tiled in the y and z
directions, with the communication of boundary elements handled by
Message Passing Interface (MPI). Time stepping is
via a third order Runge-Kutta method. The code's modular structure
allows a flexible selection of various physical
processes and variables, making it easily adaptable for many types of
MHD problems, including spherical dynamos. We
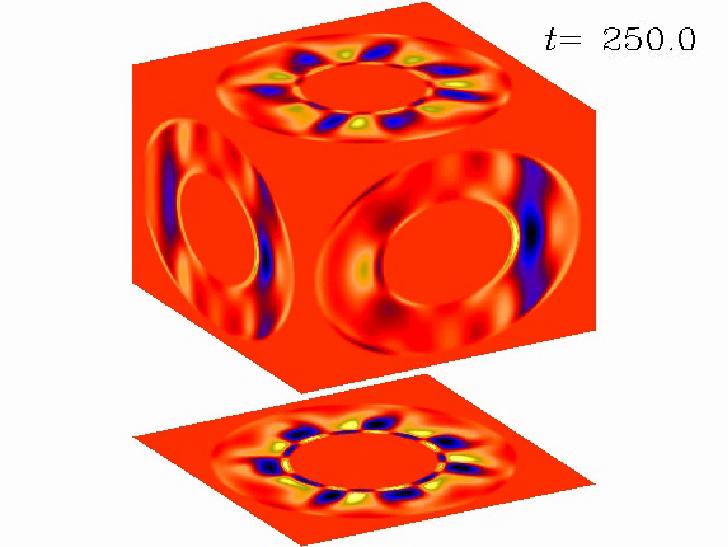
demonstrate dynamo action driven by thermal convection in a spherical
shell of ideal gas, for comparison with Kageyama
et al. (Phys. Plasmas, 2, 1421-1431, 1995). More realistic modelling of
terrestrial dynamos requires the implementation
of Boussinesq or anelastic approximations. We report on our progress in
this direction, and initial attempts to
reproduce the geodynamo benchmark (Christensen et al., Phys. Earth
Planet. Int., 128, 25-34, 2001) by this approach.