Taking advantage of the properties of liquid metals and of rapidly
rotating
flows, we are able to compute dynamos at high Reynolds number (Re >
100 000)
and low magnetic Prandtl number (Pm < 0.01)
We developped a numerical model that uses a quasi-goestrophic
approximation
to compute the flow (whithout subgrid scale model), leading to
two-dimensional equations.
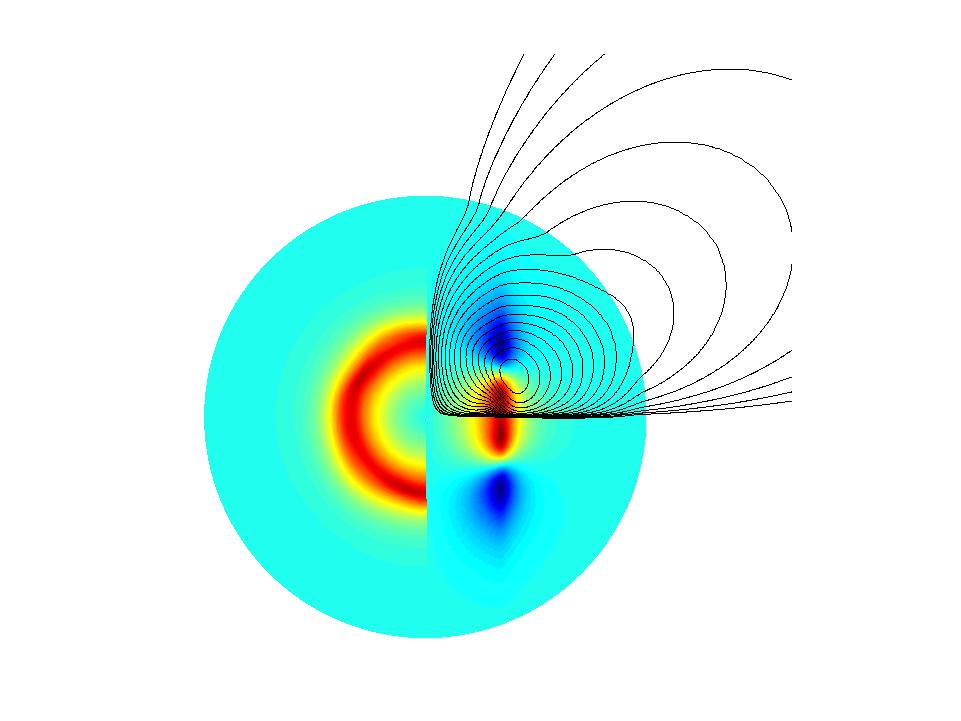
The induction equation for the magnetic field is fully resolved in 3D,
in a sphere.
This approach proves quite efficient for low magnetic Prandtl number and
suitable flows, for which there is a scale separation between magnetic
field and
velocity field, allowing to compute the magnetic field on a coarser
grid and whith
larger time steps than for the velocity field.
We show results of these calculations applied on the turbulent flow
produced by
the destabilization of a Stewartson shear layer.