Chapitre 4
5.1 Quelques particularités
Première page
En 1848, Heinrich Schwabe (1789-1875) annonça pour la première fois
que le
nombre de taches solaires qu'il observait depuis 1826, variait avec une
périodicité probable de 10 ans. Rudolph Wolf (1816-1893) confirma la
découverte de Schwabe en étudiant toutes les données disponibles sur les
taches. Il affina la période moyenne du cycle à 11 ans et en 1848, il
introduisit le nombre relatif de taches (plus connu sous le nom de nombre de
Wolf ou de Zürich), , qu'il définit ainsi :
où
est le nombre de régions perturbées (soit par des groupes, soit
par des taches individuelles),
le nombre de taches
individuelles et
un coefficient personnel. La valeur de ce coefficient
dépend de la méthode de l'observateur pour le comptage des taches et leur
subdivision en groupes, de la taille du télescope, du grossissement
employé, des conditions d'observation, etc. Pour ses observations, Wolf lui
attribua une valeur de 1, puis en 1882, ses successeurs, introduisant un
changement dans la méthode de comptage, lui donnent une valeur de 0,6.
Actuellement, le centre de Zurich qui reprend l'ensemble des données des
différents observatoires, attribue à chacun d'eux une valeur pour
de façon à rendre les mesures homogènes.
Wolf a multiplié le nombre de groupes par 10 afin de donner plus
d'importance à l'apparition d'un nouveau groupe qu'à celle d'une
nouvelle tache dans
un groupe. La séparation des taches en groupes peut être difficile en
période de forte activité, lorsque plusieurs groupes apparaissent les uns
à côté des autres ou lorsqu'ils dessinent des structures complexes.
Dans ce cas, des règles (données par Künzel), spécifiant quelques
caractéristiques des groupes et taches, peuvent aider à leur
classification.
La valeur journalière de ne donne qu'une indication quant au nombre de
taches présentes sur l'hémisphère visible. Du fait de la rotation solaire
cette valeur varie d'un jour à l'autre. De plus, le facteur 10
attribué au nombre de régions perturbées peut augmenter considérablement
la valeur de
simplement par l'apparition d'une tache isolée
supplémentaire d'un jour à l'autre. Une moyenne annuelle du nombre de
Wolf constitue donc une meilleure représentation
du niveau d'activité.
La définition de est par ailleurs assez arbitraire : même dans des
conditions d'observations similaires, plusieurs observateurs peuvent obtenir
des valeurs de
et de
différentes.
La mesure de l'aire occupée par
les taches est par conséquent plus objective. Elle a été mesurée
photographiquement à l'observatoire royal de Greenwich depuis 1876.
Le nombre
de Wolf a cependant l'avantage considérable de la longueur de la
série temporelle (figure 5.1) puisque les taches ont été
répertoriées régulièrement depuis le tout début du XVIII
siècle.
Le nombre de Wolf est un indicateur partiellement quantitatif reflétant généralement l'activité globale sur le Soleil. Il permet de tester des modèles théoriques sur des échelles de temps relativement grandes. L'activité solaire ayant un impact certain sur l'atmosphère terrestre, il est aussi possible qu'elle en est un sur l'évolution du climat. Les analyses actuelles du cycle solaire révélées par le nombre de Wolf se tournent donc vers les études des relations entre données climatiques et données solaires. Si de telles relations existent, les modélisations de la variation du nombre de Wolf pouvant conduire à des simulations du niveau de l'activité solaire dans le futur ou dans le passé, il serait, théoriquement, possible de reconstruire l'évolution climatique passée et de la prédire. Nous pourrions alors savoir si le Soleil a réellement eu un rôle important lors de la période de refroidissement terrestre qui fut répertoriée sur les régions de l'Atlantique Nord. Rappelons que simultanément à ce ``petit âge glaciaire'' (de 1640 à 1705), peu de taches furent visibles sur le Soleil (minimum de Maunder, de 1645 à 1715).
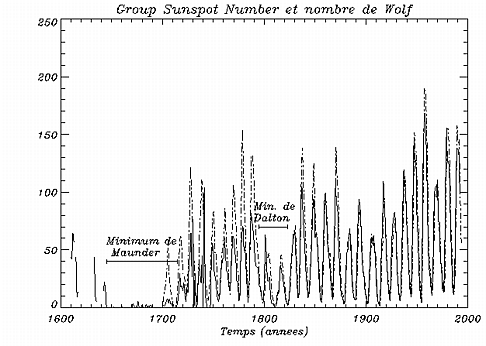
Récemment, Hoyt et al. (1994) ont introduit un nouvel indicateur de
l'activité qu'ils ont appelé le
Group Sunspot Number.
Leur série temporelle est une reconstruction objective et homogène du
nombre de Wolf, basée
uniquement sur des nombres de groupes. En effet,
Hoyt et Schatten (1992) ont montré que 90 % de la variabilité du
nombre de Wolf était attribuable aux variations dans le nombre de groupes.
Par ailleurs,
Schaefer (1993) a montré que le nombre de Wolf pouvait être égal à un
multiple du nombre de groupes.
Le nombre de groupe de taches (à partir duquel est calculé le Group Sunspot
Number) a été calculé à partir de 349000 observations journalières
obtenues par plus de 350 observateurs entre 1610 et 1993.
Afin de rendre les mesures homogènes, Hoyt et al. utilisent les
données de l'observatoire royal de Greenwich comme
référence (disponibles de 1874 à 1976 et considérées comme les plus
fiables)
et normalisent toutes les autres observations à cette série
temporelle. Ils obtiennent donc un ensemble de données qui aurait
été identique à celui de Greenwich si Greenwich avait observé
continuellement entre 1610 et 1993. Ils déduisent de cette série le Group
Sunspot Number en égalant la moyenne de leur nombre de groupes entre 1874 et
1991 avec celle du nombre de Wolf pour la même période. Pour que les
moyennes soient identiques, il est nécessaire de multiplier leur nombre de
groupes par 11,93.
Leur Group Sunspot Number (voisin en moyenne du nombre de Wolf) est alors
ainsi défini : où
est le nombre de groupes
de taches qui aurait été compté si Greenwich avait observé.
Le nombre de Wolf
et leur Group Sunspot Number
est
à peu près identique à partir de 1870 environ. Il y a en revanche de
sérieuses différences pour les décades antérieures,
étant
systématiquement plus petit que le nombre de Wolf.
est représenté sur
la figure 5.1 (en trait continu) de même que le nombre de Wolf (en
traits pointillés) par comparaison.
Sur la figure 5.2 sont représentées les transformées de ces deux indicateurs de l'activité : en trait continu est dessinée la transformée de Fourier du Group Sunspot Number et en trait pointillé, celle du nombre de Wolf. Les séries temporelles ont été découpées en quatre parties qui se chevauchent. Cela permet de constater que l'amplitude du pic correspondant à l'oscillation de 11 ans ou à celle du cycle de Gleissberg (80 ans environ) varie avec le temps. Ce n'est que sur les données récentes que le cycle de 11 ans est le plus actif. Les différences entre les analyses spectrales des deux séries temporelles sont appréciables pour les deux graphiques du haut et s'atténuent considérablement à partir de 1891.
Chapitre 4
5.1 Quelques particularités
Première page
vig@
