Atmospheric parameters relevant to high angular resolution observing Fried's coherence length Wavefront outer scale Lo Wavefront inner scale lo Characteristic time t Isoplanatic angle and spectral bandwidth

Fried's coherence length:
It can be defined as the diameter of a wavefront area over which the rms phase variations due to atmosphere are equal to 1 rad. A more strict definition relates ro to the phase structure function DÞ (r) which under Kolmogorov law must be of the form: The relation of ro to the refractive index structure coefficient C²N(h) (optical energy of the turbulence) and wavelength l for observations at zenith(Roddier 1981) is:
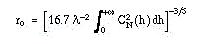where h is the altitude of the turbulent layers.

Wavefront outer scale Lo:
In the turbulence theory the outer scale Lo is considered as a parameter that defines the greatest size of eddies. The phase structure function of a wavefront passed through a single turbulent layer saturates at r > Lo. So the Kolmogorov's law, which is the background of the theory of astronomical image formation through the terrestrial atmosphere, is valid only in the so-called inertial range lo < r < Lo (denotes wavefront inner scale) Various expressions for DÞ (r) that take into account its saturation at larger r can be found in the literature (Lutomirski 1971).
In reality the light passes through many turbulent layers of different strengths and different £o Their combined effects on the wavefront is characterized by a spatial coherence outer scale of the wavefront (Borgnino 1990) called also wavefront outer scale Lo. It is related to the geophysical outer scale of different turbulent layers Lo by a weighting formula:

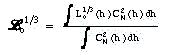The parameter £o is relevant to the operation of long-baseline interferometers because the atmospheric optical path length variations depend on it. Thus it is very desirable to have a £o monitor near the interferometers. Conversely,£o can be measured directly with an interferometer. Such estimates have been published by Mariotti et al. (1984), Colavita et al. (1987), and Busher et al. (1991). The optical path length in an interferometer depends not only on the atmospheric phase differences but also on the instrument itself (thermal drifts, mechanical errors, etc.). So direct interferometric measurements of £o is not a very clear method, and also a very expensive one. A less direct but more robust approach is the comparison of angle of arrival measured at different parts of the wavefront. Several attempts of this kind were made with wavefront sampling on a telescope aperture (Tallon, 1989; Rousset et al. 1991; Ziad et al. 1993). The extension of this technique to greater baselines is the main task of G.S.M. We must mention here an early attempt of this kind (Ataev et al. 1982).

Wavefront inner scale lo:
It represents roughly the smallest eddy size occuring naturally maintained against viscous dissipation and consequently it yields the rate of dissipation for the turbulent kinetic energy, which is one of the parameters allowing the determination of turbulence fluxes of momentum and heat particularly in the atmospheric surface layer. In addition, the inner scale is of interest because the precise knowledge of the air refractive-index spectrum in the dissipation range is important for atmospheric optical propagation studies, for example in the case of weak or very strong scintillation. Their estimation appears so of interest as well in the field of Optics in random medium as in the one of Micrometeorology
As in the outer scale case, is well to underline the difference between the optical parameter lo, spatial coherence inner scale of the perturbed wavefront reaching the ground level, and the local geophysical parameter lo(h), inner scale of turbulence varying from one turbulent layer to another.

Characteristic time t:
The temporal evolution of atmospheric disturbances places severe limit on the exposure time of an interferometer or an adaptive optics wavefront sensor and hence limits their sensitivity. If wind and turbulence altitude profiles v(h) and C²N(h) were known, t could be evaluated theoretically (Roddier & Léna 1984a; Lopez 1992). The corresponding expressionsdiffer for different observing techniques. For speckle interferometry t =0.36 ro/Dv where Dv is ameasure of v(h) dispersion with a suitable C²N(h) weighting (Roddier et al. 1982). For small-aperture interferometry and adaptive optics the characteristic time is estimated as t= 0.31 ro/v*, where v* is some average wind speed. In typical conditions both expressions for t lead to similar estimates. Unfortunately they cannot be used in most cases because wind and C²N(h) height profiles are not known. Direct optical measurements of t are thus of great value.

Isoplanatic angle and spectral bandwidth
For the sake of completeness we mention here two other atmospheric parameters relevant to H.A.R observing. The isoplanatic angle defines the usable field of view in stellar interferometry and depends directly on C²N(h) profile which can be measured by in situ soundings or using SCIDAR (i.e Scintillation Detection and Ranging) (Vernin & Azouit 1983).
The spectral bandwidth of an interferometer is also related to atmospheric corrugations of the wavefront (Roddier & Léna 1984b).Given ro and £o it can be calculated and hence no special monitor is required for its measurement.