2.1.1 Stabilité convective

Considérons une bulle de gaz déplacée adiabatiquement de sa position d'équilibre. Si elle monte, alors sa position d'équilibre d'origine était instable ; si elle descend, c'est que sa position d'équilibre d'origine était stable. Le critère définissant les conditions pour une telle stabilité ou instabilité a été énoncé pour la première fois par Schwarzschild en 1906.

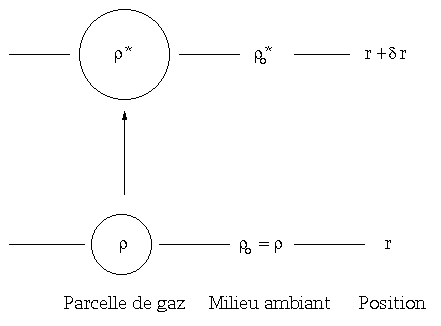
Soient la densité de la bulle à la distance , et la densité du milieu environnant la bulle (voir la figure 2.1). La bulle parcoure un trajet , elle a alors une densité et baigne dans le milieu ambiant de densité . Supposons que le mouvement soit suffisament rapide pour qu'il soit adiabatique, mais encore suffisament lent pour que la pression interne de la bulle s'ajuste à la pression locale. La condition d'instabilité est alors :

La flottabilité (buoyancy force) augmente et la bulle monte de plus en plus rapidement. Le développement au premier ordre de l'équation (2.1) amène à :

où est le gradient de densité sous des conditions adiabatiques. En se limitant au cas où la pression est donnée par l'équation des gaz parfaits : (avec , poids moyen moléculaire) et en imposant un équilibre de pression, le critère d'instabilité devient :

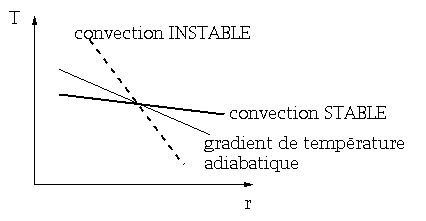
Dans le Soleil . Pour que la convection devienne instable, le gradient de température doit donc être plus important, dans le sens, plus négatif, que le gradient de température adiabatique.
Dans l'enveloppe solaire, les petites variations de sont conséquentes à l'ionisation partielle de l'hydrogène et de l'hélium. Dans ce cas, est fonction de et de . En supposant que lors du trajet de la bulle de gaz vers le haut, l'équilibre d'ionisation soit instantannément ajusté, alors le poids moléculaire à l'intérieur de la parcelle de gaz est la même fonction de et de que celui à l'extérieur.

En substituant (2.4) dans (2.3), on obtient :

ou encore :

où : et est la valeur adiabatique de (figure 2.2).

Lorsque le critère de Schwarzschild est cité, il est fait référence à l'équation (2.6). Les conditions exprimée ci-dessus sont à la fois suffisantes (Schwarzschild 1906) et nécessaires (Lebovitz 1966) pour une instabilité convective dans une zone de convection externe (c'est-à-dire aux endroits tels que ).