3.3.5 Quelques exemples
Application
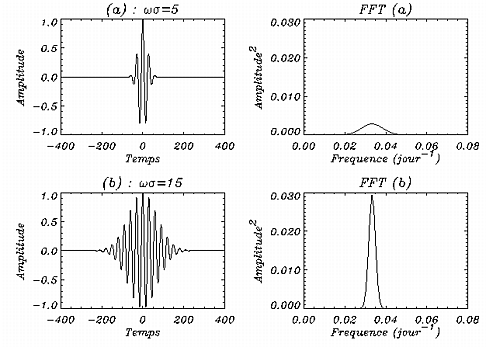
La première figure
(figure 1.8)
représente une
ondelette de Morlet pour deux valeurs du produit
(
).
En fait, c'est le paramètre
qui change, puisque la
puissance des deux spectres est centrée autour de la même fréquence.
Cette variation dans le paramètre délocalise un peu l'ondelette
puisque le nombre d'oscillations est plus grand. En revanche, ce dernier
point a pour effet bien évident d'augmenter la résolution en fréquence.
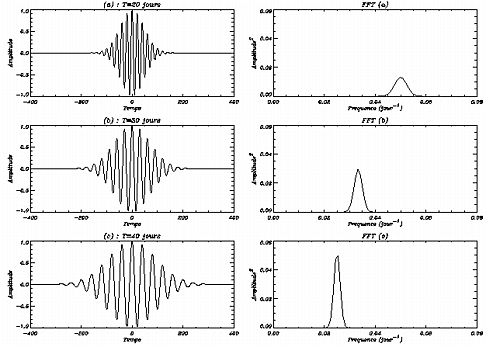
La figure suivante (figure 1.9) illustre l'effet de
la dilatation de l'ondelette de Morlet dans le domaine fréquentiel.
Le nombre d'oscillations restant le même, l'ondelette s'étent
davantage, la résolution temporelle est donc moins
bonne. Cette dilatation équivaut à un changement de fréquence,
ce qui se note sur les représentations des transformées de Fourier
de ces ondelettes (à droite) : le pic de puissance est chaque fois
centré sur la fréquence correspondant à celle de l'ondelette.
Ces figures indiquent que la perte de résolution temporelle se
fait au profit de la résolution fréquentielle.
Au paragraphe 3.2.2 il a été vu que la transformée de Fourier
avait du mal à analyser un signal dont la fréquence variait dans
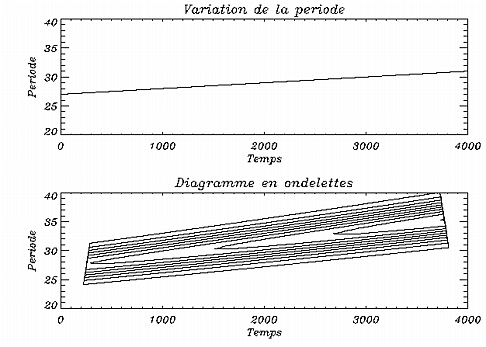
le temps (se reporter à la figure 1.6). La figure
1.10 représente sur le dessin du haut la variation
temporelle de la période de ce signal et sur celui du bas
son diagramme en ondelettes. En ordonnées du diagramme en ondelettes
sont portées les périodes correspondant aux diverses dilatations
de l'ondelette pour lesquelles l'analyse a été faite. Le temps
est porté en abcisse. On voit donc les courbes de niveau des variations
du module de la transformée en ondelettes. Ces courbes indiquent que
la période varie de 28 à 35 jours environ alors que sa
variation a été fixée entre 27 et 31 jours (voir le schéma du
haut de la figure 1.10). Le module de la transformée
en ondelette n'est pas sensible à la fréquence instantanée
mais à la pente des variations qu'elle admet (c'est-à-dire à sa
dérivée). Il est par conséquent difficile de donner des valeurs
aux périodicités qui peuvent ressortir dans ce genre de diagramme.
Il est en revanche possible de dire si la période évolue dans le
temps ou si elle dispara^t ou réappara^t brusquement.
3.3.5 Quelques exemples
Application
vig@
Wed Oct 30 19:17:13 MET 1996