5.1.1 Variations temporelles

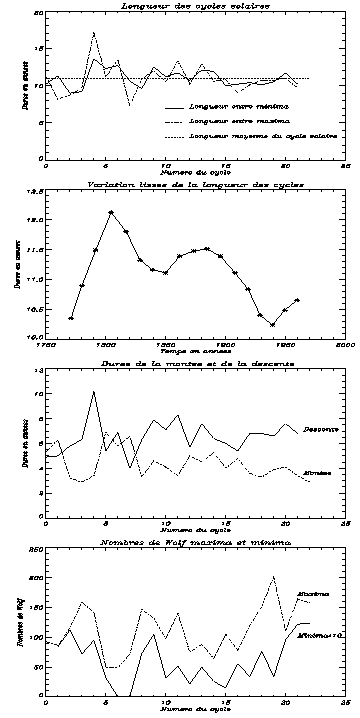
La variation du nombre de Wolf est assez régulière pour que l'on puisse la qualifier de cyclique. Chaque cycle est assorti d'un numéro. Le cycle numéro 0 est celui qui com-mence en 1745 et prend fin en 1755. Nous en sommes actuellement (août 1996) au tout début du cycle 23. Il faut préciser que la fin du cycle 22 n'est pas encore définitivement déterminée. Par ailleurs, nous avons vu au chapitre 2 que la définition d'un cycle était quelque peu arbitraire puisque d'après le diagramme de papillon les cycles se chevauchent. La figure 5.3 montre que chaque cycle est différent. La longueur des cycles varie, ainsi que leur maximum et minimum, de même que la durée de la montée et de la descente. Les variations de la longueur du cycle sont plus grandes si la longueur est estimée entre deux maximums que si elle est calculée entre deux minimums. La longueur du cycle est en général déterminée entre deux minimums car ceux-ci sont plus stables que les maximums (lorsque l'activité est à son maximum, la variation du nombre de Wolf est très importante). La longueur du cycle ainsi calculée varie entre 9 et 13,6 ans. Si cette longueur est lissée par le filtre [1,2,2,2,1] (introduit par Gleissberg), on note que la longueur des cycles a une tendance nette à décro^tre. Par ailleurs, plus la montée du cycle est rapide et plus le nombre de Wolf maximum sera grand. En moyenne, la durée de l'ascension est de 4,4 ans, celle de la descente est de 6,5 ans. De plus, une activité importante implique en moyenne un cycle court alors que les cycles solaires longs sont représentatifs d'un faible activité. Gleissberg en 1852 montra que la variation de la longueur du cycle (ou du nombre maximal de Wolf) était systématique et qu'elle évoluait avec une période comprise entre 80 et 90 ans (cycle de Gleissberg). Ces caractéristiques des cycles peuvent permettre de prédire le niveau de l'activité solaire.

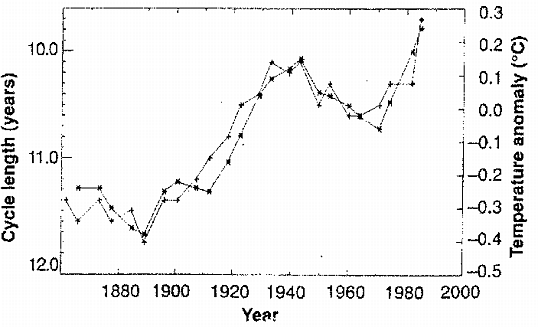
Par ailleurs, Friis-Christensen et Lassen (1991, 1994) ont montré que la longueur des cycles était corrélée avec l'anomalie (relative à l'intervalle 1951-1980) de température terrestre (au sol) de l'hémisphère Nord (figure 5.4) qui semble être l'indicateur de température globale le plus fiable car c'est le plus grand ensemble de mesures systématiques disponibles. Butler (1994) confirme cette corrélation en prenant comme indicateur global, les températures moyennes obtenues continuemment à l'observatoire d'Armagh (Irlande du Nord). Cette corrélation permet d'étudier l'influence de l'activité solaire sur le climat terrestre. C'est une autre raison d'étude du nombre de Wolf : une prédiction de ce dernier et/ou une meilleure compréhension des phénomènes qui régissent ses variations pourraient permettre de prédire en conséquence l'évolution climatique.

A l'aide d'une analyse en ondelettes, Ochadlick et al. (1993) ont étudié la variation de la période du cycle solaire ainsi que celle du cycle de Gleissberg. Ils trouvent effectivement que la période du cycle n'est pas constante et suggèrent de plus que le cycle de Gleissberg peut également varier dans le temps. Leur analyse révèle aussi l'existence d'une oscillation de période comprise entre 50 et 70 ans présente entre 1700 et 1800 puis entre 1860 et 1930.