5.1.2 Le minimum de Maunder

La théorie dynamo du cycle solaire est confrontée à de nombreuses difficultés pour l'explication du comportement observé de l'activité des taches. Nous venons de voir en particulier l'existence d'une irrégularité dans la séquence des cycles de 11 ans. Mais le fait observationel le plus impressionnant est la soudaine disparition des taches durant la période 1645-1715 (minimum de Maunder). La meilleure confirmation de l'existence du minimum de Maunder est donnée par l'évolution temporelle de l'abondance passée du C assimilé dans les troncs d'arbre. L'évolution temporelle de ce radio-isotope montre de plus que ce minimum n'est pas unique : il y a eu le minimum de Spörer (1420-1530), le minimum de Wolf (1280-1340) et le minimum de Oort (1010-1050). La distance moyenne entre ces minimums est de 190 ans, mais elle n'est pas caractéristique d'une période ou quasi-période puisqu'il n'y a pas de grand minimum en 1880 (Ruzmaikin 1981). Cette suppression de l'activité (sous forme de taches) doit cependant être une caractéristique naturelle de l'évolution temporelle de l'étoile puisque non seulement elle appara^t de temps à autre, mais de plus environ 10 à 15 %des étoiles de type solaire ne montrent pas d'activité (dans les raies H et K du calcium) (Baliunas 1991). Selon les séries temporelles d'indices terrestres de l'activité solaire, telles celles du C ou du Be, les cycles solaires de période de 11 ans survivent durant les grands minimums mais avec une faible amplitude, c'est-à-dire que peu d'évênements dus aux champs magnétiques forts apparaissent à la surface. Nous avons vu au chapitre 3 qu'en revanche, les variations du rayon étaient bien plus prononcées qu'elles ne le sont actuellement. De plus des aurores boréales ont été observées durant le minimum de Maunder ce qui aurait tendance à montrer que l'activité magnétique était toujours présente bien que faible.

La disparition des taches sur le Soleil fut un phénomène remarquable et remarqué par les scientifiques de l'époque. Il est en effet bien établi à présent que l'absence de taches n'est pas due à une absence d'observation puisqu'on compte plus de 8000 jours d'observations sur la période de 70 ans du minimum de Maunder (Hoyt et al. 1994, Ribes et al. 1988a). Weiss et Weiss (1979) notent de plus qu'il semblerait que même les non-astronomes aient été au courant de cette disparition des taches puisque Marwell dans un poème satirique adressé au roi y fait allusion.

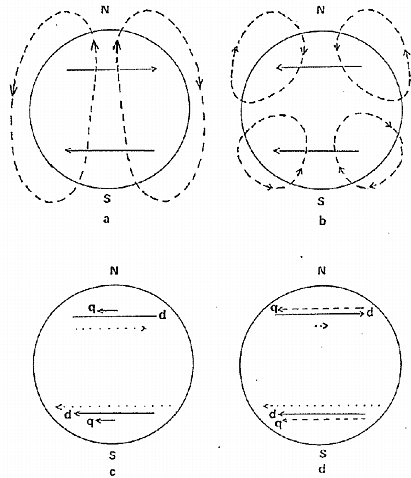
Les observations montrant une irrégularité dans les cycles solaires et l'apparition soudaine de minimums prolongés de l'activité, ne peuvent s'expliquer ni par une périodicité régulière ni par une séquence de fluctuations aléatoires. L'explication de ces phénomènes requière une théorie de la dynamo non linéaire. Le champ magnétique global solaire (champ polodal) peut être très schématiquement représenté par un dipôle. Dans un régime non linéaire, un champ magnétique azimuthal peut être généré par un dipôle dominant et un quadripôle faible. Ceci pourrait expliquer l'existence d'une asymétrie entre le nombre de taches de l'hémisphère Nord et de l'hémisphère Sud. Un aspect très intéressant de cette dynamo non linéaire est l'existence d'une autre solution pour laquelle le quadripôle et le dipôle ont des forces comparables (figure 5.5). Ce cas implique l'absence de tache dans un hémisphère entier et un diagramme de papillon réduit à l'autre hémisphère. Une telle situation a pu survenir durant le minimum de Maunder, puisque les seules rares taches observées (une centaine) le furent dans l'hémisphère Sud uniquement et qu'elles étaient de plus confinées dans une zone proche de l'équateur (Sokoloff et Nesme-Ribes 1994 et références internes).

Par ailleurs, certains auteurs tentent d'expliquer l'irrégularité des cycles solaires par des modèles chaotiques de faible dimension (Feynman et Gabriel 1990, Mundt et al. 1991, Morfill et al. 1991, Pavlos et al. 1992, Carbonell et al. 1994). Un chaos de faible dimension (les différentes analyses mènent à des valeurs pour la plupart comprises entre 2 et 3) est un compromis entre la périodicité à 11 ans du nombre de Wolf et l'irrégularité visible dans la séquence des maximums et dans la période des cycles. Des modèles chaotiques reproduisent assez bien ce comportement sans permettre toutefois une représentation fidèle de tout ce qui est observé.