Study of the monthly dispersion of the data

Since we are especially interested in the long-term irradiance variability and its relation to solar magnetic activity, any changes shorter than the solar rotational period have been considered as ``noise'' and removed from the data by calculating monthly averages in a similar way as published by Vigouroux and Delache (1994). This uncertainty of the monthly averages, called dispersion (DISP), is calculated from the corresponding daily values, analogue to the calculations of the STD standard deviations:

where represents the daily data within 30 days and their 30-day mean.

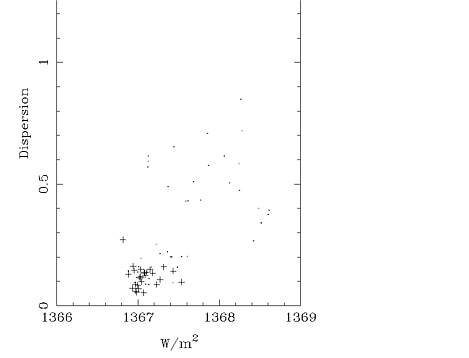
As can be seen, the dispersion values are higher during active-Sun conditions, similar to the scatter plot diagrams of the STD and ACRIM I daily irradiance values presented in Figure 6.12a and Figure 6.13c. Since in this case the ``uncertainty'', the calculated dispersion, means real solar variability, this confirms that the higher standard deviation of the ACRIM I data during higher solar activity is related more to solar effects than to instrumental uncertainties. Although the crosses, representing solar minimum activity values, are concentrated around the 1367 minimum irradiance value, the difference between their maximum and minimum values exceeds 0.5 (note that the full range of the observed solar cycle variability in the monthly averages of ACRIM total irradiance is about 1.8 ). To further examine the change of the dispersion over the solar cycle and to establish the real time of solar minimum for total solar irradiance, the dispersion diagrams have been plotted on a yearly basis (Figure 6.16).

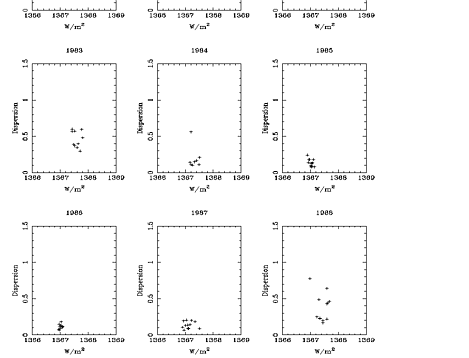
As can be seen from Figure 6.16, there is an obvious pattern in the ACRIM I dispersion diagrams and this pattern changes as a function of the solar cycle. During solar minimum the dispersion values form a concentrated cluster of data, this feature is the most pronounced during 1986. It is interesting to note that towards maximum activity conditions this cluster is less and less compressed and the variability within the cluster shows a larger range between 0.5 and 1.4 . Since the dispersion represents the daily fluctuation around the monthly mean value of the particular solar index, the variation within a particular cluster is related to the short-term variations, presumably due to aggregate fluctuation in radiances from all surface structures seen on the visible solar disk. Therefore, study of the shape and rate of compression of the dispersion clusters may provide an additional and useful tool to estimate and predict the time of maximum and minimum solar activity conditions for solar total and UV irradiances at various wavelengths as well as for additional solar parameters.

The dispersion values have also been calculated for the Mg c/w, PSI and magnetic flux values to clarify whether the cluster structure found in the case of the ACRIM data is a general pattern for other solar indices. To directly compare the temporal variation of total solar irradiance and the Mg c/w ratio, the effect of sunspots has been removed from total irradiance by means of the PSI function. The time series of total irradiance corrected for sunspot darkening ( = ACRIM I + PSI), the Mg c/w ratio, PSI and the full disk magnetic flux are presented in Figures 6.17(a) to (d). It is interesting to note that while the maximum activity level for the Mg c/w ratio is almost identical during solar cycles 21 and 22, the strength of the magnetic flux is much higher during the maximum of cycle 22 than during cycle 21. An additional difference is obvious from these time series: the Mg c/w ratio reaches maximum activity values before the magnetic flux during both solar cycles. In addition, both Mg c/w ratio and total irradiance corrected for sunspot darkening start to rise prior to the magnetic flux at the beginning of the ascending phase of solar cycle 22.

We note that similar clusters have been found in the Nimbus-7/ERB total irradiance, the PSI and the full disk magnetic flux, indicating that the dispersion diagrams provide a helpful tool in studying long-term changes in various solar activity indices. In the discussion to follow we will examine the dispersion diagrams during minimum solar activity conditions to better estimate the minimum time of solar total irradiance, the Mg c/w ratio and the measures of the solar magnetic activity. Figure 6.20 shows the dispersion diagrams for the ACRIM I total irradiance (a), (b), Mg c/w (c), PSI (d), and the magnetic flux (e). The dots represent data for 1984, crosses for 1985, diamonds for 1986, and stars for 1987. As the distribution of the dots (data for 1984) shows in Figure 6.20, part of 1984 belonged to the declining portion of solar cycle 21. The beginning of the minimum of solar cycle 21 has been determined for each data set by studying the distribution of the dots on a monthly basis. The ending date of solar minimum has been determined in a similar fashion: the distribution of stars (representing data points for 1987) made it possible to determine whether these data belonged to the cluster of minimum activity values. The estimated solar minimum intervals (beginning and ending dates) and the length of the minimum of solar cycle 21 for solar total irradiance, the Mg c/w ratio as well as for the magnetic surrogates are listed in Table 6.5. As can be seen from Table 6.5, the length of solar minimum is much shorter in the case of solar total and UV irradiance at 280 nm than in the case of solar indices representing strong magnetic field, such as the full disk magnetic flux and PSI.

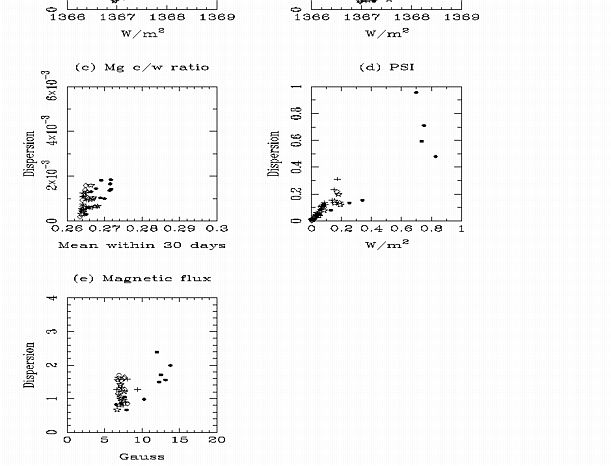
As can be seen from Figures 6.21(a)-(e), the relation between the dispersion and the monthly averages of the data is quite different for solar minimum and active-Sun conditions. In the case of solar irradiance (both bolometric and the UV flux at 280 nm) as well as the magnetic flux data, the minimum values are concentrated along almost a vertical line indicating the fluctuations of these data around their mean at the time of solar minimum. In contrast, in the case of the PSI function the regression lines for both quiet- and active-Sun conditions converge towards zero because the value of PSI is always zero in the absence of sunspots, independent of the phase of the solar activity cycle. Another interesting feature can be recognized in these dispersion diagrams, namely the scatter of the data is much larger for higher data values. This arises from the larger variability in the data during solar maximum due to the changes on active region time scales. This feature is most obvious in the case of the Mg c/w. The distribution of the maximum values of the Mg c/w ratio is related to the several years long maximum activity of both solar cycles 21 and 22, as has already been seen in Figure 6.16.