Champ toro- poloidal La dynamo cinématique 2.2.2 Cycle solaire et ...

Equation d'induction magnétique moyenne

La solution de ce problème est d'abord cherchée en terme de champ magnétique moyen. Le champ magnétique de (2.15) se compose donc de sa moyenne d'ensemble et de ses fluctuations . Il en est de même pour la vitesse de (2.15) : où représente la partie irrégulière ou turbulente des mouvements convectifs. Dans l'approximation cinématique, on suppose que le champ de vitesse est complètement déterminé et que les propriétés des fluctuations sont connues. En remplaçant et par leurs expressions données ci-dessus, en séparant les échelles entre les composantes moyennes et les fluctuations, en négligeant les termes du second ordre dans les quantités de fluctuations et en exprimant le champ électrique moyen des fluctuations () comme une fonction de et de , l'équation d'induction du champ moyen s'écrit finalement :

où

avec

L'équation (2.16) se distingue de l'équation d'induction magnétique originale de deux façons différentes. La première est que la diffusitivité magnétique a augmenté de façon conséquente. En premier ordre de grandeur, de (2.18) on a :

car et le nombre de Reynolds magnétique est très supérieur à 1 dans la zone de convection.

La deuxième différence entre les deux équations est l'introduction du terme impliquant , aussi appelé l'``effet ''.

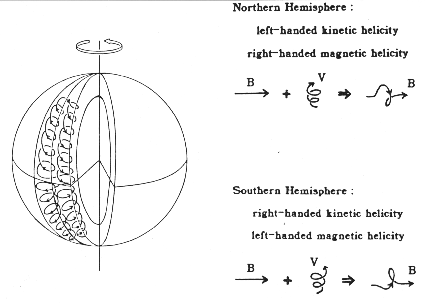
Cette expression indique que pour avoir un effet , le mouvement doit être hélicoidal c'est-à-dire que doit être corrélé à sa propre vorticité . Krause, en 1967, a montré que dans la zone de convection, les effets de la stratification de la densité et de la force de Coriolis se combinent afin de produire un tel mouvement. En effet, une parcelle de gaz montante ou descendante acquière, de par l'action des forces de Coriolis, un mouvement hélicodal dans le même sens. Ceci revient à dire que l'effet enroule les lignes de force du champ autour d'elles-même (figure 2.7). peut alors s'exprimer sous la forme :

où est la vitesse angulaire moyenne du Soleil. Le signe de est opposé à celui de la vitesse (qui est arbitrairement négative dans l'hémisphère Nord et positive dans l'hémisphère Sud) et sa valeur dépend de l'échelle de variations du champ. Cette échelle variant beaucoup dans la zone convective, il est difficile de donner une valeur à .