Equation d'induction La dynamo migrante 2.2.2 Cycle solaire et ...

La dynamo cinématique

L'effet est capable à lui seul de générer un champ magnétique moyen. Mais les solutions les plus intéressantes sont obtenues en leur combinant la rotation différentielle. Il est supposé qu'il n'y a pas de mouvements moyens exception faite de la rotation, fonction de la latitude. La séparation du champ moyen en sa composante polodale et torodale permet d'obtenir deux équations d'induction magnétique correspondant aux deux composantes du champ à partir de (2.16). Les équations obtenues peuvent être décrites par :

où : et est une fonction des variables entre les paranthèses.
Les champs polodal et torodal ont été définis par leur coordonnées polaires :
et .

L'équation (2.22) montre le rôle crucial de . En effet, si était nul, le champ polodal diminuerait de façon exponentielle à cause de la nature diffuse de cette équation. Dans ces conditions, le champ torodal serait amené à disparaitre lui aussi pour la même raison. A partir de (2.23), le champ toroidal est généré à partir du champ polodal par l'intermédiaire de la rotation différentielle (de sa dérivée pour être précis) et de l'effet . En fait, dans les modèles solaires, cet effet est négligé, la condition étant que . Bien que la valeur de ne soit pas vraiment connue (suivant les auteurs, varie entre quelques centimètres par seconde et 100 m/s), cette hypothèse serait probablement justifiée.

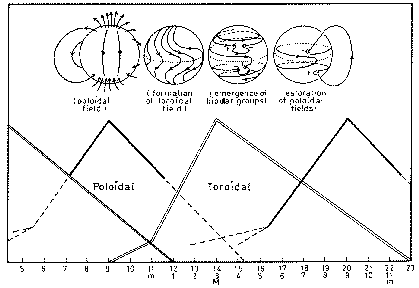
La regénération du cycle peut donc se schématiser (figure 2.8) ainsi : C'est ce que l'on appelle la dynamo , en ajoutant cinématique car on suppose que et sont des fonctions données de et de .