3.2 Analyse de Fourier
3.2.2 Quelques exemples
Les échantillonnages étudiés se font à période 
. Le
signal de départ continu est donc multiplié par la fonction
d'échantillonnage 
.
La transformée de Fourier devient donc :
où 
est la transformée de Fourier de et 
celle de 
. 
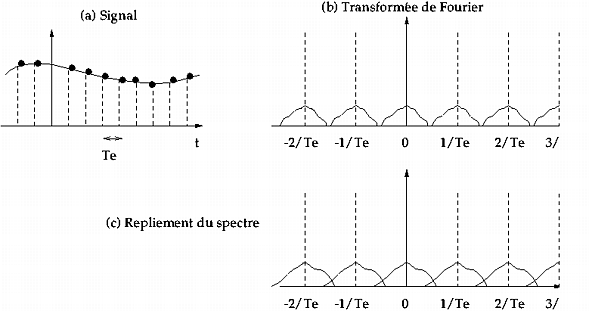
est donc périodique de période
. Afin d'éviter que le spectre ne se replie par rapport aux
axes de symétrie (voir figure 1.3), il est nécessaire
que le signal ne comporte aucune fréquence supérieure à 
.
Remarquons que le bruit peut avoir des fréquences supérieures à
. Afin d'éviter son repliement, il faut faire un filtrage analogique
(qui ne doit pas pour autant déformer le signal)
coupant dans la région avant de rentrer dans le
dispositif d'échantillonnage.
3.2 Analyse de Fourier
3.2.2 Quelques exemples
vig@
Wed Oct 30 19:17:13 MET 1996