3.3.3 Algorithme de Mallat

L'algorithme de Mallat décrit une transformation en ondelettes discrètes en utilisant l'analyse multirésolution.

Les fluctuations du signal entre deux échelles sont notées et définies par . Pour analyser plus finement ces détails, on désigne par le supplémentaire orthogonal de dans : . Alors il existe au moins une fonction appartenant à et telle que () soit une base orthonormée de . L'ensemble doit former une base de . Il est alors possible de décomposer toute fonction de sur :

Par changement de variables on a :

En posant :

est la réponse impulsionnelle du filtre discret associé . L'expression des fluctuations est alors :

Les détails à une échelle donnée sont donc des combinaisons linéaires des ``fluctuations élémentaires'' que sont les ondelettes rapportées à cette échelle.

La fonction est liée, par sa transformée de Fourier, à la transformée de Fourier de la fonction d'échelle par :

où :

Par transformée de Fourier inverse, on obtient donc :

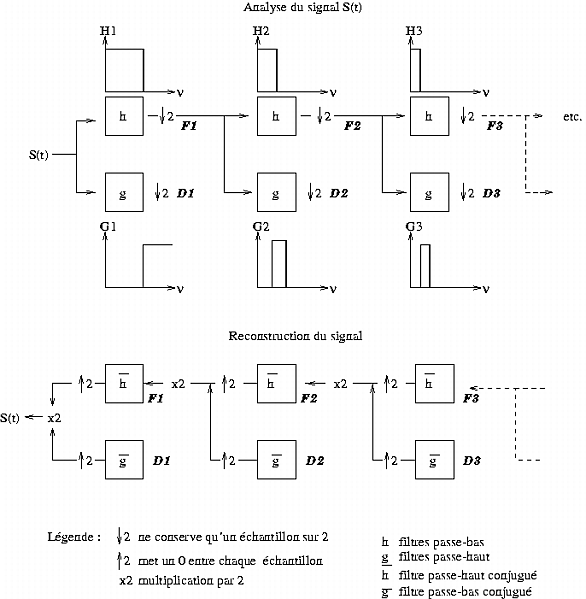
avec . Le filtre est donc un filtre passe-haut ayant la même fréquence de coupure que le filtre . et sont appelés des filtres miroirs conjugués, la relation de quadrature étant définie par (1.36). Ces deux filtres sont efficaces pour calculer la décomposition d'un signal dans une base orthonormée d'ondelettes. Le signal à analyser y est représenté par un ensemble de détails et une approximation qui correspond à la dernière résolution (figure 1.7) : c'est ce qui est appelé la représentation en ondelettes du signal.

• Reconstruction
• Ondelettes biorthogonales