5.2 Étude de la dispersion journalière des mesures

L'étude du rayon solaire mesuré au CERGA (Vigouroux et Delache 1993, voir le chapitre 4)) ayant prouvé la supériorité de l'analyse en ondelettes par rapport à l'analyse de Fourier, nous avons décidé d'appliquer la même technique au nombre de Wolf. Nous avions à notre disposition le nombre de Wolf journalier (de janvier 1874 à décembre 1982) et le nombre de Wolf mensuel (de janvier 1749 à décembre 1992). Une analyse de Fourier des données mensuelles révèle l'existence d'un battement à 11 ans. Ce battement est visible si l'on a suffisamment de cycles de 11 ans. La première périodicité étant de 11,01 ans, la seconde de 10,03 ans, le nombre de périodes nécessaires pour voir le battement est donné par : où est la résolution en fréquence c'est-à-dire 2/4096 et l'inverse de 11 ans exprimé en mois. Le calcul conduit à périodes c'est-à-dire qu'il faut un minimum de 165 ans de données si l'on veut voir le battement à 11 ans. Pour cette raison, nous avons choisi de travailler avec le nombre de Wolf mensuel (244 ans de données).

L'objectif de l'étude était d'affecter un degré de confiance aux éléments significatifs contenus dans le plan de la transformée en ondelettes ou de Fourier compte tenu des propriétés statistiques des données. Il est ensuite possible de reconstruire les données originales à partir uniquement des éléments significatifs par une transformation de Fourier ou en ondelettes inverse.

Il n'y a cependant a priori pas d'incertitudes affectées au nombre de Wolf mensuel. Toutefois, le Soleil peut montrer en un mois une variabilité journalière très grande (en particulier lors du maximum de l'activité solaire). Par conséquent, les variations journalières peuvent ne pas être entièrement déterministes. Dans un certain sens, il est donc possible de considérer que le nombre de Wolf mensuel a sa propre incertitude liée aux variations jour-à-jour à l'intérieur d'un mois. Nous avons donc dans un premier temps cherché à associer à chaque valeur mensuelle, une dispersion calculée à partir des valeurs journalières pour le mois correspondant. Il fallait aussi tenter de trouver une relation entre les valeurs moyennes (mensuelles) et les dispersions de façon à pouvoir associer par la suite à chaque valeur du fichier mensuel (depuis 1749) une dispersion correspondante.

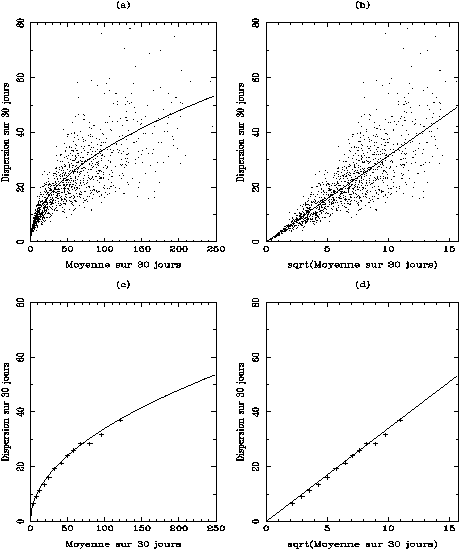
Nous avons donc dans un premier temps effectué une moyenne glissante sur 30 jours () du fichier des valeurs journalières (disponibles depuis 1874) et nous avons calculé la dispersion () de ces valeurs journalières pour chaque moyenne. La représentation graphique des dispersions en fonction des valeurs moyennes (figure 5.6) montre l'existence d'une relation entre ces deux quantités. Si l'on dessine la dispersion en fonction de la racine carrée de la valeur moyenne, cette relation devient évidente et peut se trouver sous la forme : . Les paramètres et se calculent par la méthode des moindres carrés . Mais la corrélation entre le modèle et les valeurs originales est seulement de 0,954. Nous avons donc choisi de répartir les points originaux en un certain nombre de classes d'activité, de façon à calculer le modèle sur un nombre de points plus faible, ce qui a pour effet d'augmenter la précision du calcul des paramètres. A chaque classe d'activité correspondra donc une valeur moyenne des , et une valeur moyenne des . Les classes d'activité doivent contenir approximativement le même nombre de points et doivent satisfaire deux conditions :

• le nombre de points de chaque classe doit être suffisamment grand de façon à assurer la validité de la description statistique ;
• l'écart moyen entre deux classes successives doit être plus petit que la valeur des dispersions de chaque classe, sinon la dispersion moyenne associée à chaque classe refléterait trop l'écart entre les valeurs moyennes des classes.
  

De ce compromis résulte la classification en 15 tranches des nombres de Wolf moyennés sur 30 jours. Le coefficient de corrélation entre le modèle calculé à partir de ces classes et les points correspondant à ces dernières est à présent égal à 0,998. La valeur de (ordonnée à l'origine) est approximativement nulle, celle de est de 3,39. Une telle relation entre moyenne et dispersion est typique d'une distribution de Poisson. 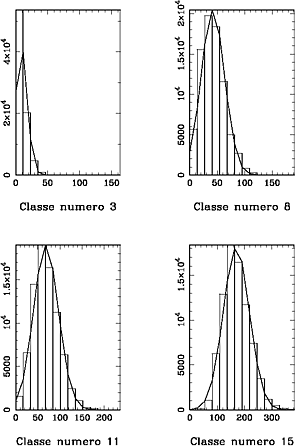Pour s'en convaincre il suffit de calculer la densité de probabilité ( variant de 1 à 15) des valeurs journalières pour chaque classe d'activité . Chaque peut être modélisée par une distribution de Poisson si cette distribution est calculée sur une quantité égale à (figure 5.7 et table 5.1). On notera que le coefficient est le même pour toutes les classes.

Cette étude confirme le modèle d'apparition des taches sur le Soleil proposé par Morfill et al. (1991). Ces auteurs avaient effectivement suggéré qu'une distribution de Poisson pouvait simuler le comportement de l'activité solaire sur des durées de l'ordre d'une rotation solaire, ce qui correspond assez bien au mois sur lequel ont été moyennées les valeurs journalières du nombre de Wolf.

Lors de la rédaction de l'article relatif à ce travail (Vigouroux et Delache 1994), nous n'avions pas d'explication pour la valeur de . Un travail ultérieur sur le nombre de groupes de taches m'a cependant permis d'en trouver une. Le nombre de groupe de taches journaliers, fourni simultanément avec le nombre de Wolf, couvre la période comprise entre 1874 et 1982. Pour l'étude de ce nombre de groupes, j'ai suivi la même procédure que pour l'analyse du nombre de Wolf journalier. Une moyenne glissante sur 30 jours () a d'abord été calculée ainsi que les dispersions () correspondantes des valeurs journalières sur 30 jours. La même procédure de réduction des données originales en 15 classes d'activité a ensuite été suivie. Le calcul par moindres carrés du modèle de l'ensemble des 15 points donnant la dispersion en fonction de la racine carrée de la moyenne a cependant donné une valeur du paramètre de 0,98 (le paramètre étant pratiquement nul). Ce n'est donc pas le nombre de Wolf ou de taches qui varie selon une loi de Poisson sur des durées de l'ordre du mois, mais le nombre de groupes. Or, nous avons vu plus haut que Hoyt et al. (1994) avaient calculé un nouvel indicateur de l'activité appelé le Group Sunspot Number. Rappelons que la moyenne de cet indicateur est égale à celle du nombre de Wolf sur la période 1874-1991. De plus, le Group Sunspot Number () est égal à 11,93 fois le nombre de groupe de taches reconstruit par Hoyt et al.. En estimant que le nombre journalier de Wolf est approximativement égal au Group Sunspot Number, alors si la relation pour le nombre de groupe entre dispersion et moyenne est : , la relation entre dispersion et moyenne pour le nombre de Wolf s'écrit : avec : qui est la valeur trouvée pour le paramètre . La valeur de (reliant le nombre moyen de Wolf sur trente jours à la dispersion des valeurs journalières correspondantes) est donc parfaitement expliquée.

Nous disposons à présent d'une relation entre les valeurs moyennées sur 30 jours du nombre de Wolf et leur dispersion correspondante. Il est donc possible d'associer à chaque valeur mensuelle disponible de 1749 à 1992, une valeur correspondante de la dispersion sur le mois, en sachant que les valeurs journalières sur cette durée sont représentatives d'une distribution de Poisson.