5.3 Analyse du cycle solaire

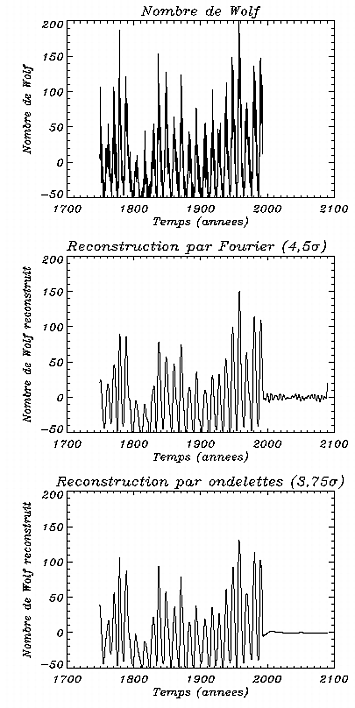
La série temporelle analysée est celle des valeurs mensuelles disponibles de janvier 1749 à décembre 1992. Dans l'article relatif à cette étude (Vigouroux et Delache 1994) nous n'avions pris que les 2048 derniers points de cette série. J'ai donc repris l'analyse de la série complète. Afin de conserver les bénéfices de la FFT (Fast Fourier Transform), j'ai complété par des zéros la série temporelle jusqu'à avoir au total 2^12=4096 points.

Il s'agit donc de comparer les mérites de la transformée de Fourier et de celle en ondelettes lorsque l'on ne veut garder qu'un certain nombre de paramètres significatifs. Les détails de cette analyse comparatives peuvent se trouver au chapitre 4 puisqu'il s'agit de la même méthode que celle appliquée à la série temporelle du rayon solaire.

Dans un premier temps, plusieurs séries temporelles aléatoires (200) ont été construites : chacune d'entre elle contient le même nombre de points que la série originale (4096). À chaque point , la valeur est tirée aléatoirement à partir d'une distribution de Poisson dont la dispersion est celle prévalant au point , mais la distribution est centrée autour d'une constante (choisie égale à 0 par des raisons de facilité). Il est alors possible d'estimer l'amplitude du bruit dans le plan de Fourier ou dans celui des ondelettes en faisant la transformée de Fourier ou en ondelettes des 200 signaux aléatoires qui ne transportent aucun signal. À chaque point de la transformée (de Fourier ou en ondelettes), on peut alors calculer un seuil statistique au-dessus duquel une amplitude peut être considérée comme significative.

Dans un second temps, 200 autres séries temporelles aléatoires ont été construites de façon identique aux précédentes, mais cette fois, à chaque point des différentes séries, la valeur est tirée aléatoirement à partir d'une distribution de Poisson centrée autour de la valeur du signal original au point (la dispersion est toujours celle prévalant au point ). On dispose ainsi de 200 signaux bruités de même allure générale que le signal original du nombre de Wolf mensuel. Le seuillage à x- des transformées (en ondelettes et de Fourier) de ces 200 signaux permettra de ne retenir que les parties significatives des transformées. L'inversion de la transformée moyenne (de Fourier ou en ondelettes) des éléments significatifs fournira une reconstruction ``lissée'' du signal original.

L'algorithme choisi pour la transformée en ondelettes est le même que celui utilisé pour l'analyse de la série temporelle du rayon solaire : il s'agit de l'algorithme de Mallat et l'on se sert des filtres miroirs quadratifs (voir les chapitres 3 et 4 pour plus de détails).

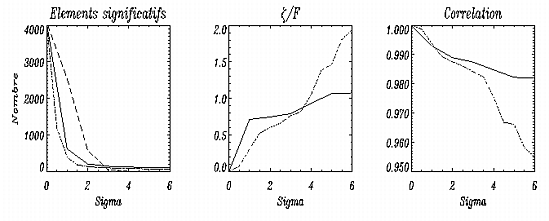
La figure 5.8 représente quelques quantités obtenues en sélectionnant les éléments significatifs des transformées pour des seuils compris entre 1 et 6. De même que dans le cas de l'analyse du rayon (et que dans le cas de l'analyse des 2048 derniers éléments du fichier mensuel original), pour un même seuil, la transformée en ondelettes nécessite moins de paramètres que la transformée de Fourier pour représenter le signal (voir le premier graphe de la figure 5.8). Cette particularité des ondelettes est cependant moins prononcée dans le cas du nombre de Wolf que dans celui du rayon probablement parce que le cycle de 11 ans est de nature quasi-périodique.

La représentation optimale du signal original sera obtenue lorsque les résidus seront de l'ordre de grandeur du nombre de degrés de liberté (qui est égal à la différence entre le nombre de points de la transformée, soit 4096, et le nombre de paramètres significatifs). Le résidu entre la série originale et la reconstruction est défini comme étant :

où les sont les données originales, les sont les points reconstruits correspondants et les sont les inverses des carrés des dispersions, fournissant ainsi un poids adéquat à chaque point (2928 points mensuels). Le deuxième graphe de la figure 5.8 montre l'évolution du rapport (multiplié par 4096/2928 pour tenir compte du fait que les transformées ont été faites sur 4096 points) en fonction du seuil. La valeur optimale (égale à 1) est obtenue à 3,75 pour l'analyse en ondelettes et à 4,5 pour celle par Fourier. Cela est probablement dû au fait que la transformée de Fourier a besoin d'un critère plus sévère dans son processus de sélection des éléments significatifs. En effet, à chaque fréquence retenue est associée une sinusode qui peut correspondre à ce qui existe dans les données originales à certains endroits mais ne plus correspondre à d'autres. Notons par ailleurs que le nombre de paramètres retenus par les ondelettes à 3,75 (2,12 %) est encore plus petit que celui obtenu par l'analyse de Fourier à 4,5 (2,78 %).

La qualité de la reconstruction est donnée par le calcul du coefficient de corrélation entre les données originales et les reconstructions :

Le troisième schéma de la figure 5.8 représente l'évolution de ce coefficient de corrélation pour des seuils compris entre 1 et 6. Les valeurs sont toutes plus ou moins du même ordre de grandeur jusqu'à un de 3,75. Le coefficient de corrélation calculé pour la reconstruction en ondelettes diminue beaucoup à partir de 3,75. Parallèlement, le rapport augmente et devient nettement supérieur à 1 alors que le nombre de paramètres significatifs pour des supérieurs à 3,75 n'évolue pas beaucoup. Cela veut dire qu'après 3,75, le seuillage supprime des éléments nécessaires à la reconstruction, ce qui a pour effet d'augmenter les résidus par rapport au nombre de degré de liberté (ceux-ci sont en nombre insuffisant pour bien représenter le signal) et de diminuer le coefficient de corrélation (il n'y a plus d'adéquation entre signal original et signal reconstruit). En revanche, le rapport et le coefficient de corrélation obtenus par analyse de Fourier atteignent un pallier à 5. Il faut en effet que le seuil soit plus sévère que 5 pour que des paramètres nécessaires à la représentation du signal soient supprimés bien que le processus de seuillage continue de fonctionner et donc d'enlever quelques pics. Ceci indique que le processus de seuillage de la transformée de Fourier retient plus de paramètres que ceux nécessaires à la stricte reconstruction du signal.

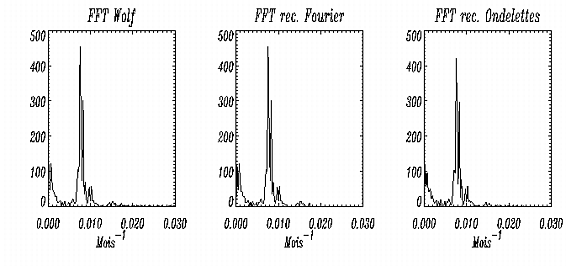
La quasi-périodicité à 11 ans est visible dans les spectres des reconstructions aussi bien que dans celui du signal original (figure 5.10). Pour les deux reconstructions, tous les pics du spectre correspondant à des fréquences inférieures à (0,018 mois) (c'est-à-dire à des périodicités supérieures à 5 ans) sont considérés comme significatifs. Par conséquent, les deux analyses (de Fourier et en ondelettes) montrent que dans le cas du nombre de Wolf, l'information pertinente est contenue dans une large bande de fréquences (sans oublier les informations liées à la phase des oscillations correspondantes). Une description purement modale des données comme des interférences entre des oscillations stables constitue donc une sélection biaisée de l'information réelle contenue dans le signal. En ce qui concerne le cycle de 11 ans, il est préférable d'abandonner la représentation en terme de modes indépendants et de passer à une description dans un plan temps-fréquence ou une description incluant une large bande spectrale. Les données disponibles ne nous permettent pas de décider entre ces deux représentations. Elles sont probablement équivalentes si tous les éléments significatifs sont retenus.

Nous avons vu dans ce chapitre que l'étude du nombre de Wolf peut révéler l'existence d'un système dynamique sinon complexe du moins non trivial. Ces études sont importantes non seulement pour mieux comprendre les mécanismes qui régissent l'activité solaire mais aussi pour permettre de vérifier ou d'infirmer une relation entre activité solaire et climat terrestre. Ce dernier évoluant sur des échelles de temps très grandes, il est nécessaire de comparer ses variations avec une série temporelle solaire elle aussi très longue que seul le nombre de Wolf (ou plus tard, le Group Sunspot Number) peut fournir. Ce n'est bien évidemment pas le nombre de Wolf lui-même qui pourrait influencer les variations climatiques mais plutôt le flux lumineux solaire reçu sur Terre. Une mesure de ce flux lumineux par unité de surface et à une distance moyenne Terre-Soleil est disponible sous le nom d'irradiance solaire depuis 1978. Les variations de cette dernière sont pour une part dues aux taches solaires (qui réduisent le flux lumineux sur des échelles de temps de l'ordre de quelques jours) et pour une autre part dues aux éléments brillants (qui augmentent le flux lumineux sur des échelles de temps de l'ordre de quelques mois). Cette constation a conduit certains auteurs (Foukal et Lean 1990) à estimer l'irradiance à partir du nombre de Wolf (globalement représentatif de l'activité des facules) et de l'aire des taches (approximant l'effet de ces dernières). Cette approximation pourrait alors permettre la détermination de la valeur de l'irradiance lors du minimum de Maunder, et de chercher si la diminution correspondante durant cette époque avait impliqué une diminution de température sur la surface terrestre (Lean et al. 1995a). L'irradiance solaire est par conséquent un indicateur ``clé'' dans les problèmes inhérents aux relations Terre-Soleil. Cette série temporelle contemporaine de l'activité solaire est l'objet du prochain chapitre.